In 7, we showed that the energy of a particle of mass M in an L L L box in the state labeled n, m, l is E n, m, l 2 2 (n 2 m 2 l 2 ) 2ML 2 The probability of finding a particle in the state n, m, l at temperature T is given by the Boltzmann distribution P(n, m, l) exp( E n, m, l k B T) In a hot gas...

First define the probability that the particle has energy less than E max where the su ...

In ?7, we showed that the energy of a particle of mass M in an L ?

Question:

In ?7, we showed that the energy of a particle of mass M in an L ? L ? L box in the state labeled |n, m, l? is E _{n, m, l} = ?²?²(n² + m² + l²)/2ML². The probability of finding a particle in the state |n, m, l? at temperature T is given by the Boltzmann distribution P(n, m, l) ? exp(?E _{n, m, l}/k_BT). In a hot gas the energy levels are very close together, so E can be regarded as a continuous variable. Show that the probability of finding the particle with energy between E and E + dE at temperature T is given by the Maxwell?Boltzmann distribution, dP/dE = 2??Ee^?E/kBT /(?k_BT)^3/2. Employ the methods used to compute the spectrum of blackbody radiation, including eq. (22.20)?

Distribution
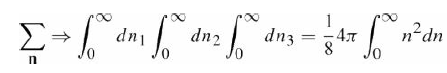
The word "distribution" has several meanings in the financial world, most of them pertaining to the payment of assets from a fund, account, or individual security to an investor or beneficiary. Retirement account distributions are among the most...

Fantastic news! We've Found the answer you've been seeking!