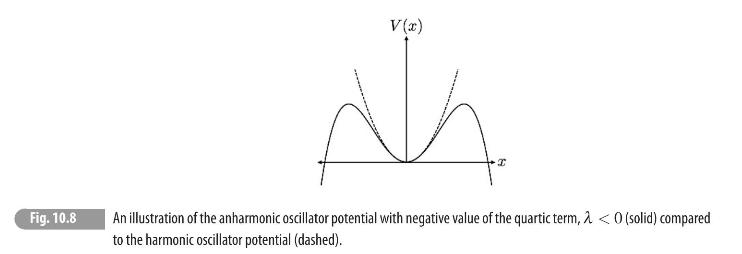
We had introduced quantum mechanical perturbation theory as analogous to the Taylor expansion. As such, one might expect that as higher and higher orders are calculated, a better approximation of the true result is achieved. However, in general, quantum mechanical perturbation theory produces a non-convergent, asymptotic series in the expansion parameter. For the anharmonic oscillator Hamiltonian of Eq. (10.128), for example, an arbitrarily small, but negative, value for \(\lambda\) destabilizes the potential. Regardless of the size of \(\lambda\), if it is negative then at large positions \(|x| \rightarrow \infty\) the potential runs to negative infinity. This destabilization with \(\lambda

Recently, techniques identified by Bender and Wu for studying the anharmonic oscillator have been packaged into a plug-in for Mathematica and can be used to extend the perturbation theory for the anharmonic oscillator and other potentials to extremely high orders. \({ }^{7}\) This program can be downloaded from https://arxiv.org/abs/1608.08256 and the associated article contains several examples. Try this program out with the anharmonic oscillator and calculate very high orders \((\sim 100)\) in perturbation theory. What do you notice 6 C. M. Bender and T. T. Wu, "Anharmonic oscillator," Phys. Rev. 184, 1231-1260 (1969).

7 T. Sulejmanpasic and M. Ünsal, "Aspects of perturbation theory in quantum mechanics: The BenderWu Mathematica ® package,” Comput. Phys. Commun. 228, 273-289 (2018) [arXiv:1608.08256 [hep-th]].

about the approximations of, say, the ground-state energy and wavefunction as the order in perturbation theory increases? Think up your own potential and estimate its energy levels with the program.

Transcribed Image Text:

Fig. 10.8 V(x) I An illustration of the anharmonic oscillator potential with negative value of the quartic term, < 0 (solid) compared to the harmonic oscillator potential (dashed).