Let N be a hypergeometric random variable having the distribution of the number of white balls in a random sample of size r from a set of w white and b blue balls. That is,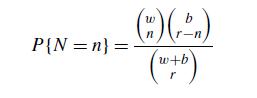

where we use the convention that m j
= 0 if either j m. Now, consider a compound random variable SN =N i=1Xi , where the Xi are positive integer valued random variables with αj = P{Xi = j }.

(a) With M as defined as in Section 3.7, find the distribution of M −1.

(b) Suppressing its dependence on

b, let Pw,r (k) = P{SN = k}, and derive a recursion equation for Pw,r (k).

(c) Use the recursion of

(b) to find Pw,r (2).

P{N=n}= b (w)(ron) (w+b)