Let X1,X2, . . . be independent continuous random variables with a common distribution function F and density f = F , and for k 1 let

Hint: Use induction. First prove it when k = 2, and then assume it for k. To prove it for k + 1, use the fact that

where the preceding used the combinatorial identity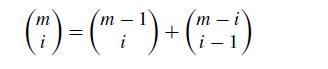

Now, use the induction hypothesis to evaluate the first term on the right side of the preceding equation.

(d) Conclude that XNk has distribution F.

Transcribed Image Text:

Nk = min{nk: X = kth largest of X1, ..., Xn} (a) Show that P{Nk=n} = (b) Argue that = k-1 n(n-1) " nk. xx (x) = f(x) (F(x))*- (i + k 2) (F(x))" fxNk (c) Prove the following identity: i=0 a-k i+k. - + k 2) (1 a)', 0