Order Statistics: Let X1, . . . , Xn be i.i.d. from a continuous distribution F, and
Question:
Order Statistics: Let X1, . . . , Xn be i.i.d. from a continuous distribution F, and let X(i) denote the ith smallest of X1, . . . , Xn, i = 1, . . . , n. Suppose we want to simulate X(1)
(a) Suppose that λ(t), the hazard rate function of F, is bounded. Show how the hazard rate method can be applied to generate the n variables in such a manner that no sorting is necessary.
Suppose now that F
−1 is easily computed.
(b) Argue that X(1), . . . , X(n) can be generated by simulating U(1)
· · ·
−1(U(i)). Explain why this means that X(i) can be generated from F
−1(βi ) where βi is beta with parameters i, n +i +1.
(c) Argue that U(1), . . . , U(n) can be generated, without any need for sorting, by simulating i.i.d. exponentials Y1, . . . , Yn+1 and then setting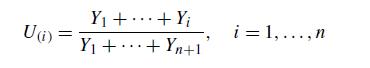
Hint: Given the time of the (n + 1)st event of a Poisson process, what can be said about the set of times of the first n events?
(d) Show that if U(n) = y then U(1), . . . , U(n−1) has the same joint distribution as the order statistics of a set of n − 1 uniform (0, y) random variables.
(e) Use part
(d) to show that U(1), . . . , U(n) can be generated as follows:
Step 1: Generate random numbers U1, . . . , Un.
Step 2: Set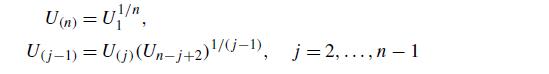
Step by Step Answer:







