Suppose that a customer of the M/M/1 system spends the amount of time x >0 waiting in
Question:
Suppose that a customer of the M/M/1 system spends the amount of time x >0 waiting in queue before entering service.
(a) Show that, conditional on the preceding, the number of other customers that were in the system when the customer arrived is distributed as 1+P, where P is a Poisson random variable with mean λ.
(b) Let W
∗
Q denote the amount of time that an M/M/1 customer spends in queue. As a by-product of your analysis in part (a), show that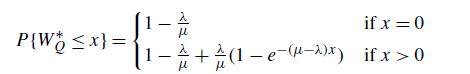
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:






