Suppose W,X1, . . . , Xn are independent nonnegative continuous random variables, with W being exponential with rate λ, and with Xi having density function fi , i = 1, . . . , n.

(a) Show that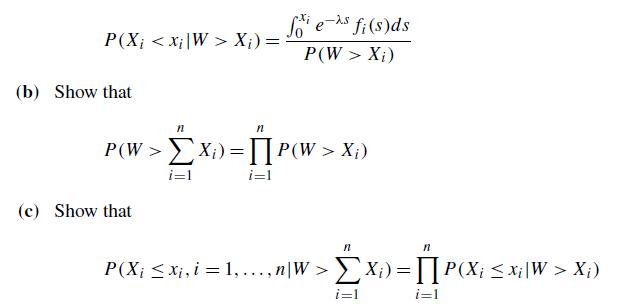

That is, given that W >
n i=1Xi , the random variables X1, . . . , Xn are independent with Xi now being distributed according to its conditional distribution given that it is less than W, i = 1, . . . , n.

Transcribed Image Text:

P(X; X;) =: fie-ks fi(s)ds P(W > Xi) (b) Show that n n P(W>X)=[[P(W > X;) i=1 i=1 (c) Show that n n P(X x, i = 1,...,n\W > X;) = [[P(Xixi|W > X;) i=1 i=1