The random variables X and Y are said to have a bivariate normal distribution if their joint
Question:
The random variables X and Y are said to have a bivariate normal distribution if their joint density function is given by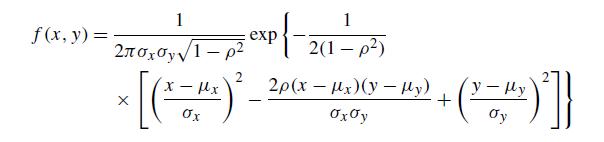
for −∞ 0,σy > 0,−∞
(a) Show that X is normally distributed with mean μx and variance σ2 x , and Y is normally distributed with mean μy and variance σ2 y .
(b) Show that the conditional density of X given that Y = y is normal with mean μx + (ρσx/σy)(y −μy ) and variance σ2 x (1 − ρ2).
The quantity ρ is called the correlation between X and Y. It can be shown that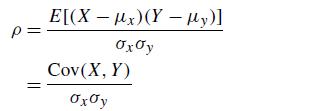
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:






