A liquid is filling a container that has the form of a cone of angle around a vertical axis (Fig. 1.9). The liquid enters

A liquid is filling a container that has the form of a cone of angle α around a vertical axis (Fig. 1.9). The liquid enters the cone from the apex through a hole of diameter d at a velocity v (t) = kt where k is a constant. When the surface of the liquid is at height h (t), the volume is

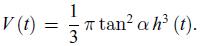
Initially, at time t = 0, the height h (0) = 0. Find an expression for the rate of change of volume V˙ (t) and determine h (t).

Figure 1.9

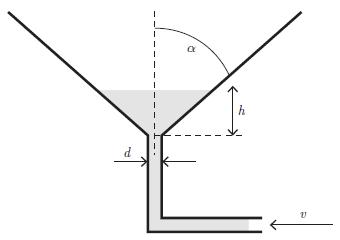
V (t) = 1 3 tan a h (t).