Determine the hydrostatic pressure p inside a droplet, as a function of its radius r (Fig. 4.11).
Question:
Determine the hydrostatic pressure p inside a droplet, as a function of its radius r (Fig. 4.11). Assume that the drop (d) forms at the end of a short thin tube mounted at the end of vertical cylindrer containing the liquid (l). When a drop forms at the end of the tube, the change in the container height is negligible. If the height of the liquid above the tip of the tube is h, then the hydrostatic pressure is p = p0 + ρgh, where ρ is the volumetric mass density of the liquid, and g characterises the gravitation at the surface of the Earth. For this liquid, the differential of the free energy reads,
![]() Show that
Show that
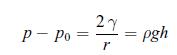 Figure 4.11
Figure 4.11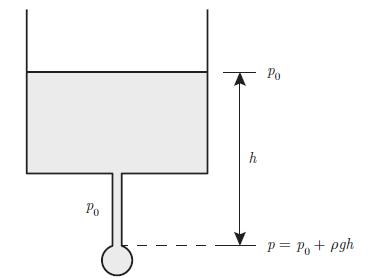
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Principles Of Thermodynamics
ISBN: 9781108426091
1st Edition
Authors: Jean-Philippe Ansermet, Sylvain D. Brechet
Question Posted:





