In this chapter, several examples of a current density in one direction inducing the gradient of an intensive quantity in another direction were shown. These effects are referred to by the name of their discoverers: Righi-Leduc (11.29), Hall (11.75), Nernst (11.85), Ettingshausen (11.80). The latter refers to a temperature gradient induced by an orthogonal electric charge current density. It was pointed out recently that this effect can occur in a crystal, which consists of two types of electric charge carriers and presents a strong crystalline anisotropy in the plane where the heat and electric charge transport take place. No magnetic induction field needs to be applied orthogonally in order to observe this effect [191]. The material has two types of electric charge carriers, electrons (e) and holes (h). Assume that no ‘chemical reaction’ takes place between them. The thermoelectric properties are isotropic, i.e. the same in all directions. Therefore, the Seebeck tensors for the electrons and holes are given by,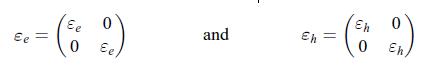However, the conductivities differ greatly in two orthogonal directions. Therefore, the conductivity tensors are given by,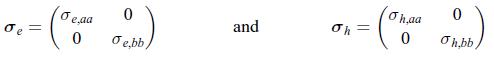where a and b label the a-axis and the b-axis that are orthogonal crystalline axes. Consider an electric charge transport along the x-axis at an angle θ from the a-axis and show that this electric current density j_q induces a heat current density j_Q along the y-axis. This is the planar Ettingshausen effect. It can be understood by establishing the following facts:a) Show that the Seebeck tensor for this crystal is given by [176],b) Show that the Seebeck tensor for this crystal is diagonal and written as,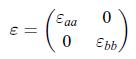where the diagonal component ε_aa is different from ε_bb in general. The matrix is given here for a vector basis along the crystalline a-axis and b-axis.

c) Write the components of the Seebeck tensor with respect to the coordinate basis (x, y),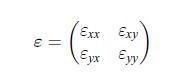in terms of the diagonal components εaa and εbb of the Seebeck tensor with respect to the coordinate basis (a, b).d) The heat current density j_Q is related to the electric charge current density j_q by, which is a local version of the Peltier effect (11.108). The Peltier tensor is related to the Seebeck tensor by,In particular, for an electric charge current density j_q = j_q,x ˆx, where ˆx is a unit vector along the x-axis, show that the component j_Q,y along the y-axis of the heat current density jQ = j_Q,x ˆx + j_Q,y ˆy, where ˆy is a unit vector along the y-axis, is given by,Thus, the planar Ettingshausen effect is maximal for an angle θ = π/4.

Transcribed Image Text:

Ee Ee Ee and 43 43 43