Continuing with Example 2.1, suppose that each of the products are required to be packed.

Every unit of product A requires 4 hours while every unit of product B needs 3.5 hours for packaging. Suppose that in the packaging department, 105 hours are available every week.

Under these conditions, what product mix would maximise the profit?

The problem can be restated as follows:

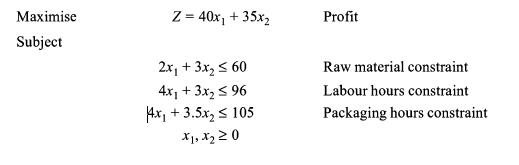
The constraints and the objective function (in the form of iso-profit line) are charted in Figure 2.5.

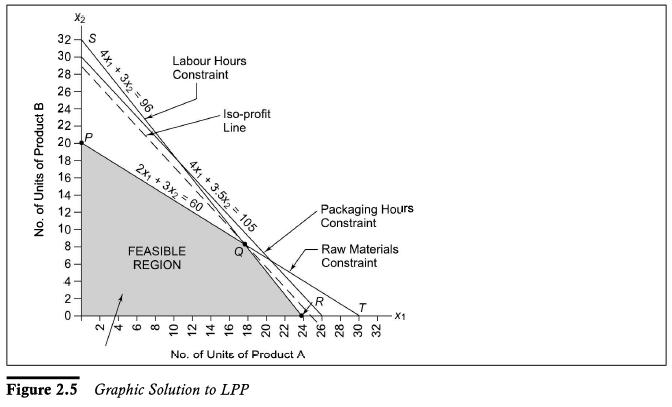
We observe that the inclusion of the packaging hours constraint does not provide a side of the polygon representing the feasible region. Thus, this constraint is of no consequence and hence is redundant. The optimal solution to the problem is the same as the optimal solution to the problem in Example 2.1. Thus, we have x1 = 18, x2 = 8 representing the optimal solution. The product mix given by this shall consume the entire 60 kg of raw material and 96 labour hours, but shall leave an unused capacity of l 05 - ( 4 x 18 + 3. 5 x 8) = 5 hours in the packaging department.

Transcribed Image Text:

Maximise Subject Z=40x1 + 35x2 Profit 2x + 3x2 60 4x1 + 3x2 96 14.x + 3.5x2 105 0 Raw material constraint Labour hours constraint Packaging hours constraint