Let (T_{0}=0, T_{1}, T_{2}, ldots) denote dates where (T_{n}) is (n) days from today (left(T_{0}ight)). An asset's

Question:

Let $T_{0}=0, T_{1}, T_{2}, \ldots$ denote dates where $T_{n}$ is $n$ days from today $\left(T_{0}ight)$. An asset's price is $\$ 1,000$ today, $A\left(T_{0}ight)=1000$, and the continuously compounded interest rate is constant, $r=4 \%$ with fractions of time calculated Act/365: $T_{i+1}-T_{i}=1 / 365$.

(a) What is the 10-day forward price of the asset, $F_{A}\left(0, T_{10}ight)$ ?

(b) You agree today $\left(T_{0}=0ight)$ to buy the asset in 10 days for $K=F_{A}\left(0, T_{10}ight)$. How much do you need to pay/receive today to enter into this contract?

(c) Assume the asset's price increases by $\$ 10$ each day for the next 10 days, $A\left(T_{n}ight)=A(0)+10 n$, and compute the missing entries in the following table where $C_{F u t}$ is the cash flow for one futures contract, $C F_{F w d}$ is the cash flow for one forward contract, $Q_{\text {Fut }}$ is the number of futures contracts needed to replicate one forward contract, and $F V_{\text {Fut }}=F V(Q \times C F)$ is the corresponding cash flow of the modified futures contract, future valued to $T_{10}$.

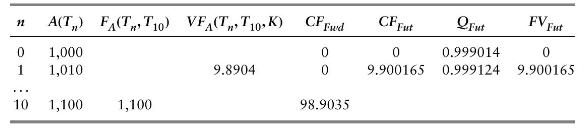
image text in transcribed