Suppose at time t = 0, we are given four zero-coupon bond prices {B1, B2, B3, B4} that mature at times t = 1, 2, 3, 4. This forms the term structure of interest rates. We also have one-period forward rates {f0, f1, f2, f3), where each fi is the rate contracted at time t = 0 on a loan that begins at time t = i and ends at time t = i + 1. In other words, if a borrower borrows $N at time t = i, he or she will pay hack N(l + ft) at lime t = i +1. The spot raw is denoted by ri. By definition we haver0 = f0The {Bi} and all forward loans arc default-free.At each tine period there are two possible stares of the world, denoted by{ui, di: = 1, 2, 3, 4}.(a) Looked at from time i = 0, how many possible states of the world are there at time i = 3?(b) Suppose{B1 = .9.B2 = .87, B3 = .82. B4 = .75}and{f0, 8%, f1 = 9%, f2 = 10%, f3 = 18%}.Form three arbitrage portfolios that will guarantee a net positive return at times i = 1, 2, 3 with no risk.(c) Form three arbitrage portfolios that will guarantee a net return at time i =0 with no risk.(d) Given a default-free zero-coupon hand, Bn, that matures at time = ii, and all the forward rates {f0 .. fn-1}, obtain a formula that expresses Br as a function of fi(e) Now consider the Fundamental Theorem of Finance as applied to the system:

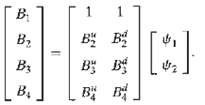
Can all Bi be determined independently?(f) In the system above can all the {fi} he determined independently?(g) Can we claim that all f1 are normally distributed? Prove youranswer.

,