Suppose you want to define a magnetic scalar potential U (Eq. 5.65), in the vicinity of a current-carrying wire. First of all, you must stay away from the wire itself (there ?? x B ?? 0); but that's not enough. Show, by applying Ampere's law to a path that starts at a and circles the wire, returning to p (Fig. 5.47), that the scalar potential cannot be single-valued (that is, U(a) ?? U(b), even if they represent the same physical point). As an example, find the scalar potential for an infinite straight wire. (To avoid a multi valued potential, you must restrict yourself to simply-connected regions that remain on one side or the other of every wire, never allowing you to go all the way around.)

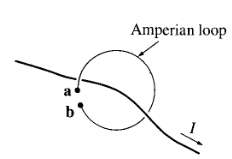
a b Amperian loop