The electrostatic problem of a point charge q outside an isolated, charged conducting sphere is equivalent to

Question:

The electrostatic problem of a point charge q outside an isolated, charged conducting sphere is equivalent to that of three charges, the original and two others, one located at the center of the sphere and another ("the image charge") inside the now imaginary sphere, on the line joining the center and the original charge. If the point charge and sphere are replaced by two conducting spheres of radii ra and rb, carrying total charges Qa and Qb, respectively, with centers separated by a distance d > ra + rb, there is an equivalence with an infinite set of charges within each sphere, one at the center and a set of images along the line joining the centers. The charges and their locations can be determined iteratively, starting with a charge qa(1) at the center of the first sphere and qb(l) correspondingly for the second sphere. The charge qb(l) has its image qa(2) within the first sphere and vice versa. Then the image charge within the first sphere induces another image within the second sphere, and so on. The sum of all the charges within each sphere must be scaled to be equal to Qa or Qb.The electrostatic potential outside the spheres, the force between the spheres, etc. can be found by summing the contributions from all the charges.(a) Show that the charges and their positions are determined iteratively by the relations,

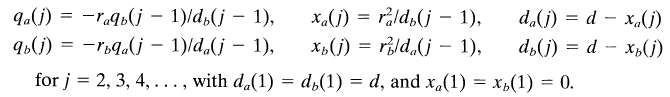
(b) Find the image charges and their locations as well as the potentials on the spheres and force between them by means of a suitable computer program. [In computing the potential on each sphere, evaluate it in different places: e.g., in the equatorial plane and at the pole opposite the other sphere. This permits a check on the equipotential of the conductor and on the accuracy of computation.] (c) As an example, show that for two equally charged spheres of the same radius R, the force between them when almost in contact is 0.6189 times the value that would be obtained if all the charge on each sphere were concentrated at its center. Show numerically and by explicit summation of the series that the capacitance of two identical conducting spheres in contact is C/4πє0R = 1.3863 ? ? ? [= In4].