The frequency of revolution of an electron in a circular orbit of radius r is frev =
Question:
The frequency of revolution of an electron in a circular orbit of radius r is frev = v/2Ï€r, where v is the speed.
(a) Show that in the nth stationary state
-1.png)
(b) Show that when n1 = n, n2 = n – 1, and n is much greater than 1,
-2.png)
(c) Use your result in part (b) and Equation 37-13 to show that in this case the frequency of radiation emitted equals the frequency of motion. This result is an example of Bohr’s correspondence principle: when n is large, so that the energy difference between adjacent states is a small fraction of the total energy, classical and quantum physics must give the same results.
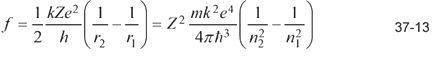
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Fundamentals of Ethics for Scientists and Engineers
ISBN: 978-0195134889
1st Edition
Authors: Edmund G. Seebauer, Robert L. Barry
Question Posted:





