The Levinson-Durbin algorithm described in section 11.3.1 solved the linear equations ? m a m? = ?
Question:
The Levinson-Durbin algorithm described in section 11.3.1 solved the linear equations
?mam?= ? ?m
where the right-hand side of this equation has elements of the autocorrelation sequence that are also elements of the matrix ?. Let us consider the more general problem of solving the linear equations
?mbm = cm
where cm is an arbitrary vector. (The vector bm is not related to the coefficients of the backward predictor.) Show that the solution to ?mbm = cm?can be obtained from a generalized Levinson-Durbin algorithm which is given recursively as
bm(m) = c(m) - ?bIm ? 1bm ? 1/Efm ? 1
bm(k) = bm ? 1(k) ? bm(m)avm ? 1(m ? k)?k = 1, 2, . . . ., m ? 1
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? m = 1, 2. . . p ?
Where bI(1) = c(1)/?xx(0) = c(1)/Ef0?and am(k) is given by (11.3.17). Thus a second recursion is required to solve the equation ?mbm = cm.
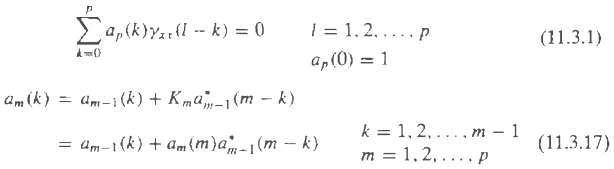
Step by Step Answer:

Digital Signal Processing
ISBN: ?978-0133737622
3rd Edition
Authors: Jonh G. Proakis, Dimitris G.Manolakis





