The one-dimensional calculation of Example 42.5 (Section 42.3) can be extended to three dimensions. For the three dimensional fcc NaC1 lattice, the result for the potential energy of a pair of Na+ and CI?? ions due to the electrostatic interaction with all of the ions in the crystal is U = ?? ae2/4??0r, where a = 1.75 is the Made lung constant. Another contribution to the potential energy is a repulsive interaction at small ionic separation T due to overlap of the electron clouds. This contribution can be represented by A/r8, where A is a positive constant, so the expression for the total potential energy is(a) Let r0 be the value of the ionic separation T for which U got is a minimum. Use this definition to find an equation that relates r0 and A, and use this to write U tot in terms of r0. For NaC1, r0 = 0.281 nm. Obtain a numerical value (in electron volts) of U tot for NaC1.(b) The quantity - U tot is the energy required to remove a Na+ ion and a C1?? ion from the crystal. Forming a pair of neutral atoms from this pair of ions involves the release of 5.14eV (the ionization energy of Na) and the expenditure of 3.61eV (the electron affinity of a). Use the result of part (a) to calculate the energy required to remove a pair of neutral Na and a atoms from the crystal the experimental value for this quantity is 6.39eV how well does your ca1culation agree?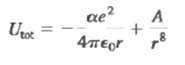

Utot ae + A 8