Question: The solution by Cramers rule to the linear system a 11 x 1 + a 12 x 2 + a 13 x 3 = b
The solution by Cramer’s rule to the linear system a11x1 + a12x2 + a13x3 = b1, a21x1 + a22x2 + a23x3 = b2, a31x1 + a32x2 + a33x3 = b3, has
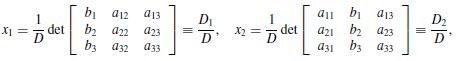
And
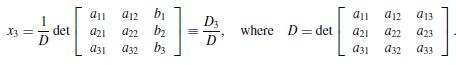
a. Find the solution to the linear system 2x1 + 3x2 − x3 = 4, x1 − 2x2 + x3 = 6, x1 − 12x2 + 5x3 = 10, by Cramer’s rule.
b. Show that the linear system 2x1 + 3x2 − x3 = 4, x1 − 2x2 + x3 = 6, −x1 − 12x2 + 5x3 = 9. does not have a solution. Compute D1, D2, and D3.
c. Show that the linear system 2x1 + 3x2 − x3 = 4, x1 − 2x2 + x3 = 6, −x1 − 12x2 + 5x3 = 10 has an infinite number of solutions. Compute D1, D2, and D3.
d. Prove that if a 3 × 3 linear system with D = 0 has solutions, then D1 = D2 = D3 = 0.
e. Determine the number of multiplications/divisions and additions/subtractions required for Cramer’s rule on a 3 × 3 system.
aj1 bi a13 azi b2 az23 b3 a33 bi a12 a13 DI 1 XI =7 det b2 a23 D' X2 = 5 det b3 a32 a33
Step by Step Solution
3.37 Rating (153 Votes )
There are 3 Steps involved in it
a The solution is x 1 0 x 2 10 and x 3 26 b We have D ... View full answer

Get step-by-step solutions from verified subject matter experts
Document Format (1 attachment)
731-M-N-A-N-L-A (657).docx
120 KBs Word File


