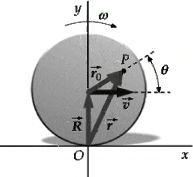
A wheel of radius R rolls without slipping at a speed V. The coordinates of the center
Question:
A wheel of radius R rolls without slipping at a speed V. The coordinates of the center of the wheel are X, Y.
(a) Show that the x and y coordinates of point P in Figure are X + r0 cos θ and R + r0 sin θ, respectively,.
(b) Show that the total velocity v of point P has the components vx = V + (r0V sin θ)/R and
vy = -(r0V cos θ)/R.
(c) Show that at the instant that X = 0, v and r are perpendicular to each other by calculating v·r.
(d) Show that v = rω, where ω = V/R is the angular velocity of the wheel. These results demonstrate that, in the case of rolling without slipping, the motion is the same as if the rolling object were instantaneously rotating about the point of contact with an angular speed w = V/R.
Step by Step Answer:

Fundamentals of Ethics for Scientists and Engineers
ISBN: 978-0195134889
1st Edition
Authors: Edmund G. Seebauer, Robert L. Barry





