0We need to remove (mathrm{H}_{2} mathrm{~S}) and (mathrm{CO}_{2}) from (1000.0 mathrm{kmol} / mathrm{h}) of a water stream...
Question:
0We need to remove \(\mathrm{H}_{2} \mathrm{~S}\) and \(\mathrm{CO}_{2}\) from \(1000.0 \mathrm{kmol} / \mathrm{h}\) of a water stream at \(0^{\circ} \mathrm{C}\) and \(15.5 \mathrm{~atm}\). 0Inlet liquid contains \(0.0024 \mathrm{~mol}_{2} \mathrm{H}_{2} \mathrm{~S}\) and \(0.0038 \mathrm{~mol} \%\) \(\mathrm{CO}_{2}\). We desire a \(99.0 \%\) recovery of \(\mathrm{H}_{2} \mathrm{~S}\) in the gas stream. Pure nitrogen at \(0^{\circ} \mathrm{C}\) and \(15.5 \mathrm{~atm}\) is used to strip out \(\mathrm{H}_{2} \mathrm{~S}\) and \(\mathrm{CO}_{2}\). Nitrogen flow rate is 3.44 \(\mathrm{kmol} / \mathrm{h}\). A staged countercurrent stripper will be used. Assume water flow rate and air flow rate are constant. Data are in Table 12-1. Note: Watch your decimals.
Table 12-1
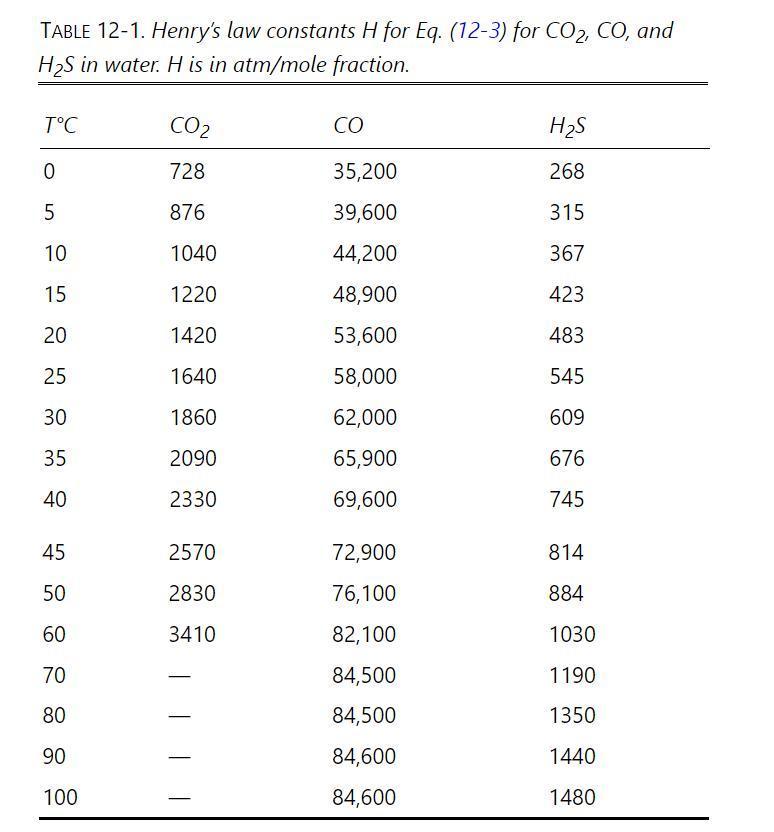
a. Determine the \(\mathrm{H}_{2} \mathrm{~S}\) mole fractions in the outlet gas and liquid streams.
b. Determine the number of equilibrium stages required.
c. Determine the \(\mathrm{CO}_{2}\) mole fraction in the outlet liquid stream.
Step by Step Answer:

Separation Process Engineering Includes Mass Transfer Analysis
ISBN: 9780137468041
5th Edition
Authors: Phillip Wankat





