A:Assume that the production technology uses labor„“and capitalkas inputs, and assume through- out this problem that the firm is currently long run profit maximizing and employing a production plan that is placing it at the lowest point of its long runACcurve.

(a) Suppose first that the technology has decreasing returns to scale but that, in order to begin producing each year, the firm has to pay a fixed license fee F. Explain why this causes the long run AC curve to be U-shaped.

(b) Draw a graph with the U-shaped AC curve from the production process described in part (a). Then add to this the short run MC and AC curves. Is the short run AC curve also U-shaped?

(c) Next, suppose that there are no fixed costs in the long run. Instead, the production process is such that the marginal product of each input is initially increasing but eventually decreasing, and the production process as a whole has initially increasing but eventually decreasing returns to scale. (A picture of such a production process was given in Graph 12.16 in the previous chapter.) Explain why the long run AC curve is U-shaped in this case.

(d) Draw another graph with the U-shaped AC curve. Then add the short run MC and AC curves. Is it possible for short run AC curves to not be U-shaped if the production process has initially increasing but eventually decreasing returns to scale?

B: Suppose first that the production process is Cobb-Douglas, characterized by the production function x = f („“,k) = A„“^αk^β with α,β > 0 and α + β < 1.

(a) In the absence of fixed costs, you should have derived in exercise 13.2 that the long run cost function for this technology is given by

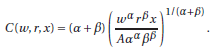
If the firm has long run fixed costs F, what is its long run average cost function? Is the average cost curve U-shaped?

(b) What is the short run cost curve for a fixed level of capital ? Is the short run average cost curve U-shaped?

(c) Now suppose that the production function is still f („“,k) = A„“^αk^β but now α+β> 1. Are long run average and marginal cost curves upward or downward sloping? Are short run average cost curves upward or downward sloping? What does your answer depend on?

(d) Next, suppose that the production technology were given by the equation

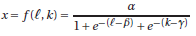
Where e is the base of the natural logarithm. (We first encountered this in exercises 12.5 and

12.6.) If capital is fixed at , what is the short run production function and what is the short

run cost function?

(e) What is the short run marginal cost function?

(f) You should have concluded in exercise 12.6 that the long run MC function is MC(w,r,x) = α(w +r )/(x(αˆ’x)) and demonstrated that the MC curve (and thus the long run AC curve) is U-shaped for the parameters α = 100, β = 5 = γ when w = r = 20. Now suppose capital is fixed at  = 8. Graph the short run MC curve and use the information to conclude whether the short run AC curve is also U-shaped.

(g) What characteristic of the this production function is responsible for your answer in part (f)?

Transcribed Image Text:

1/ (α+β) wα, χ Ααdββ wa rfx Ciw, rx) (α+ β |