A discrete-time lowpass filter is to be designed by applying the impulse invariance method to a continuous- time Butterworth filter having magnitude-squared function

The specifications for the discrete-time system are those of Example 7.2, i.e., 

0.89125 ≤ |H(e^jω) | ≤ 1,            0 ≤ |ω| ≤ 0.2 π,

|H(e^jω) | ≤ 0.17783,                   0.3π ≤ |ω| ≤ π.

 Assume, as in that example, that aliasing will not be a problem; i.e., design the continuous-time Butterworth filter to meet passband and stopband specifications as determined by the desired discrete-time filter.

(a) Sketch the tolerance bounds on the magnitude of the frequency response, |H_c(jΩ)|, of the continuous-time Butterworth filter such that after application of the impulse invariance method (i.e., h[n] = T_dh_c(nT_d)), the resulting discrete-time filter will satisfy the given design specifications. Do not assume that T_d = 1 as in Example 7.2.  

(b) Determine the integer order N and the quantity T_dΩ_c such that the continuous-time Butterworth filter exactly meets the specifications determined in part (a) at the pass band edge.

(c) Note that if T_d = 1, your answer in part (b) should give the values of N and Ω_c obtained in Example 7.2. Use this observation to determine the system function H_c (s) for T_d ≠ 1 and to argue that the system function H (z) which results from impulse invariance design with T_d ≠ 1 is the came as the result for T_d = 1given by Eq. (7.19).

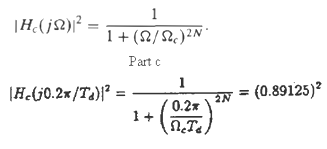
|H(j2) : 1 + (N/N)N Part c (0.89125)? |HG0.2x /T&){ = 0.2x 1+