A hollow metallic waveguide with a distortion in the form of a localized bend or increase in cross section can support nonpropagating ("bound state") configurations of fields in the vicinity of the distortion. Consider a rectangular guide that has its distortion confined to a plane, as shown in the figure, and ??₁₀ as its lowest propagating mode, with perpendicular electric field E₁ = ?. On either side of the distortion the guide is straight and of width a. Without distortion, ? = E₀ sin (?y/a) exp (? ikz), where k² = (w/?)² ? ?(?/?)². The distortion is described by a curvature k(s) = 1/R(s) and a width w(s). Locally the element of area in the plane is dA = h(s, t) ds dt, where s is the length along the guide wall and t the transverse coordinate, as shown in the figure, and h(s, t) = 1 - k(s)t. In terms of s and t the Laplacian is

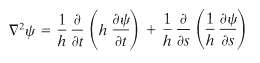
If the distortions are very small and change slowly in s on the scale of the width a, an ansatz for the solution is

[The factor in the denominator is equivalent to the factor p^?1/2 familiar from Bessel functions that converts the radial part of the Laplacian in polar coordinates to a simple second partial derivative (plus an additional term without derivatives).]

(a) Show that substitution of the ansatz into the two-dimensional wave equation, (?² + w²/?²)? = 0, leads to the equation for u(s),

if small terms are neglected. Interpret v(s) in analogy with the Schr?dinger equation in one dimension.

(b) If the distortion is in the form of a bend through an angle ? with constant radius of curvature R ? a, show that for ?a/R w₀ where

(h h s \h as at h t