A useful rule of thumb in piloting is that if the heading from your airplane to a
Question:
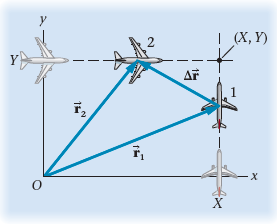
A useful rule of thumb in piloting is that if the heading from your airplane to a second airplane remains constant, the two airplanes are on a collision course. Consider the two airplanes shown in FIGURE 4-33. At time t = 0, airplane 1 is at the location (X, 0) and moving in the positive y direction; airplane 2 is at (0, Y) and moving in the positive x direction. The speed of airplane 1 is v1.
(a) What speed must airplane 2 have if the airplanes are to collide at the point (X, Y)?
(b) Assuming airplane 2 has the speed found in part (a), calculate the displacement from airplane 1 to airplane 2, Δr(vector) = r(vector)2 – r(vector)1.
(c) Use your results from part (b) to show that (Δr)y / (Δr)x = –Y/X, independent of time. This shows that Δr(vector) = r(vector)2 – r(vector)1 maintains a constant direction until the collision, as specified in the rule of thumb.
Step by Step Answer:
Set the arrival times of airplane 1 and airplane 2 equal ...View the full answer
