Ambrose, the nut and berry consumer, has a utility function U(x₁, x₂) = 4√x₁ +x₂, where x₁ is his consumption of nuts and x₂ is his consumption of berries. 

(a) The commodity bundle (25, 0) gives Ambrose a utility of 20. Other points that give him the same utility are (16, 4), (9, ___), (4, ____), (1, ____), and (0_____). Plot these points on the axes below and draw a red indifference curve through them.

(b) Suppose that the price of a unit of nuts is 1, the price of a unit of berries is 2, and Ambrose’s income is 24. Draw Ambrose’s budget line with blue ink. How many units of nuts does he choose to buy? ______ .

(c) How many units of berries? ______ .

(d) Find some points on the indifference curve that gives him a utility of 25 and sketch this indifference curve (in red).

(e) Now suppose that the prices are as before, but Ambrose’s income is 34. Draw his new budget line (with pencil). How many units of nuts will he choose? ______. How many units of berries? ______

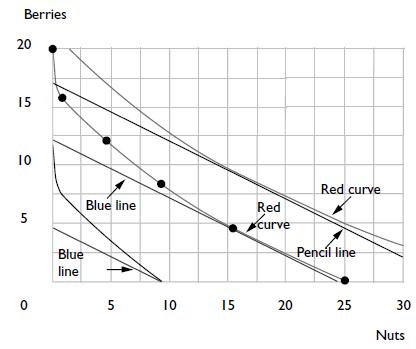
(f) Now let us explore a case where there is a “boundary solution.” Suppose that the price of nuts is still 1 and the price of berries is 2, but Ambrose’s income is only 9. Draw his budget line (in blue). Sketch the indifference curve that passes through the point (9, 0). What is the slope of his indifference curve at the point (9, 0)? −_______.

(g) What is the slope of his budget line at this point? −________.

(h) Which is steeper at this point, the budget line or the indifference curve? __________.

(i) Can Ambrose afford any bundles that he likes better than the point (9, 0)? _____.

Berries 20 15 10 Red curve Blue line Red curve Penil line Blue line 10 15 20 25 30 Nuts