Occasionally an investigator may wish to compute a confidence interval for a, the y intercept of the true regression line, or test hypotheses about a. The estimated y intercept is simply the height of the estimated line when x = 0, since a 1 b(0) = a. This implies that sa the estimated standard deviation of the statistic a, results from substituting x* = 0 in the formula for sa1bx*. The desired confidence interval is then

and a test statistic is 

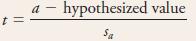
a. The article “Comparison of Winter-Nocturnal Geostationary Satellite Infrared-Surface Temperature with Shelter-Height Temperature in Florida” (Remote Sensing of the Environment [1983]: 313– 327) used the simple linear regression model to relate surface temperature as measured by a satellite (y) to actual air temperature (x) as determined from a thermocouple placed on a traversing vehicle. Selected data are given (read from a scatterplot in the article). 

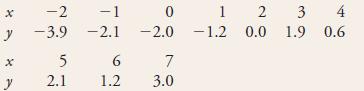
Estimate the population regression line.

b. Compute the estimated standard deviation sa. Carry out a test at level of significance .05 to see whether the y intercept of the population regression line differs from zero.

c. Compute a 95% confidence interval for a. Does the result indicate that a = 0 is plausible? Explain.

a (e critical value)s, d hypothesized value x 2 01 23 4 -3.9-2.1-2.0-1.2 0.0 1.9 0.6 7 y 2.1 1.2 3.0 6