Consider a pair of complex-valued signals s 1 (t) and s 2 (t) that are respectively represented
Question:
Consider a pair of complex-valued signals s1 (t) and s2 (t) that are respectively represented by s1 (t) = a11 ?1 (t) + a12 ?2?(t), ? ? 2 (t) = a21 ?1 (t) + a22 ?2?(t), ? ? 1 (t) and ?2 (t) are both real valued, but the coefficients a11, a12, a21, and a22 are complex valued. Prove the complex form of the Schwarz inequality, where the asterisk denotes complex conjugation. When is this relation satisfied with the equality sign?
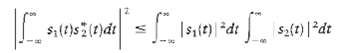
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





