Consider a signal x(n) with Fourier transform(a) Show that the signal x(n) can be recovered from its
Question:
Consider a signal x(n) with Fourier transform(a) Show that the signal x(n) can be recovered from its samples x(mD) if the sampling frequency ?x = 2?/D ? 2?m(fs = 1/D ? 2fm).(b) Show that x(n) can be reconstructed using the formula(c) Show that the bandlimited interpolation in part (b) can be thought as a two-step process: First, increasing the sampling rate by a factor of D by inserting (D ?? 1) zero samples between successive samples of the decimated signal xa(n) = x(nD) and second, filtering the resulting signal using an ideal lowpass filter with cutoff frequency ?c.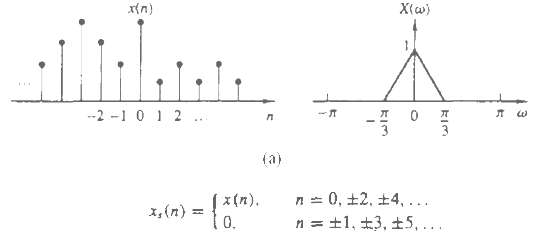
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Digital Signal Processing
ISBN: ?978-0133737622
3rd Edition
Authors: Jonh G. Proakis, Dimitris G.Manolakis
Question Posted:





