Consider the configuration of conductors of Problem 1.17, with all conductors except S₁ held at zero potential.

(a) Show that the potential ?(?) anywhere in the volume V and on any of the surfaces S_i can be written

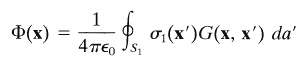
Where ?_1?(?') is the surface charge density on S₁ and G(x, x') is the Green function potential for a point charge in the presence of all the surfaces that are held at zero potential (but with S₁ absent). Show also that the electrostatic energy is

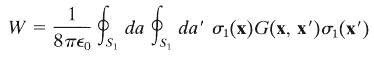
Where the integrals are only over the surface S1(b) Show that the variational expression

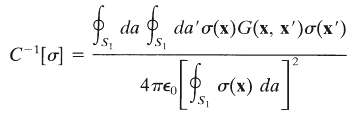
With an arbitrary integrable function ?(x) defined on S_1, is stationary for small variations of ? away from ?₁. Use Thomson's theorem to prove that the reciprocal of ?^?1[?] gives a lower bound to the true capacitance of the conductor S₁.

Transcribed Image Text:

о (х')G(х, х') da' 4 TE, JS, Ф(x)