Consider the special case of a signal constellation that has a symmetric geometry with respect to the
Question:
Consider the special case of a signal constellation that has a symmetric geometry with respect to the origin. Assume that the M message points of the constellation, pertaining to symbols m1, m2 . mm, are equally likely. Using the upper bound on the complementary error function given in Equation (5.94), show that the average probability of symbol error for the constellation is bounded as, where dik is the Euclidean distance between message points i and k, and M min is the number of transmitted signals that attain the minimum Euclidean distance for eachmi.
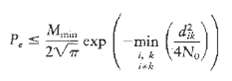
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





