Derivation of the energy equation using integral theorems, in S11.1 the energy equation is derived by accounting
Question:
Derivation of the energy equation using integral theorems, in S11.1 the energy equation is derived by accounting for the energy changes occurring in a small rectangular volume element ∆x ∆y ∆z.
(a) Repeat the derivation using an arbitrary volume element V with a fixed boundary S by following the procedure outlined in Problem 3D.1. Begin by writing the law of conservation of energy as then use the Gauss divergence theorem to convert the surface integral into a volume integral, and obtain Eq. 11.1-6.
(b) Do the analogous derivation for a moving "blob" of fluid.
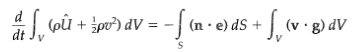
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





