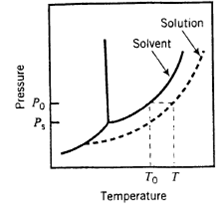
Derive Equation 6.5-4 for the boiling-point elevation of a dilute solution of a nonvolatile solute with mole fraction x in a solvent that has a pure-component vapor pressure p_s (T). To do so, suppose that when the pressure is P₀, the pure solvent boils at temperature T_b0 (so that P₀ = p_s (T_b0)] and the solvent in the solution boils at T_bs > T_b0. Further suppose that at temperature T the effective vapor pressure of the solvent is P_s = (p_s)(T_b0) < P0. (See diagram.) The procedure is as follows.

(a) Write the Clausius—Clapeyron equation (Equation 6.1-3) for P_s (the effective solvent vapor pressure at T_b0) and then for P₀ (the effective solvent vapor pressure at T_bs), assuming that at the low solute concentrations in question the heat of vaporization is the same at both temperatures. Subtract the two equations. Simplify the equation algebraically assuming that T and T are close enough together to say that T_b0 T_bs ≈ T²_b0.

(b) Substitute the Raoult’s law expression (Equation 6.5-2) for P_s = (p_s) e (T_b0). Observe that if x << 1 (which it is for highly dilute solutions), then in (1 – x) ≈ – x. The desired result follows.

Solution Solvent Po P, To Temperature Pressure