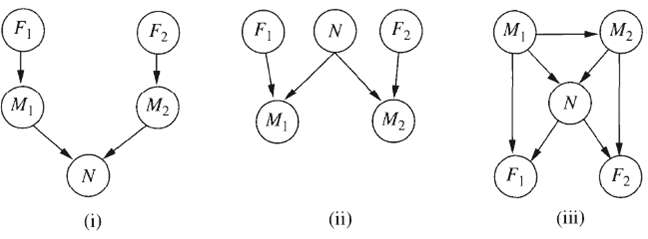
Two astronomers in different parts of the world make measurements M₁ and M₂ of the number of stars N in some small region of the sky, using their telescopes. Normally, there is a small possibility e of error by up to one star in each direction. Each telescope can also (with a much smaller probability f) be badly out of focus (events F₁ and F₂) in which case the scientist will undercount by three or more stars (or, if N is less than 3, fail to detect any stars at all). Consider the three networks shown in Figure.

a. Which of these Bayesian networks are correct (hut not necessarily efficient) representations of the preceding information?

b. Which is the best network? Explain.

c. Write out a conditional distribution for P (M₁?N), for the case where N ? {1, 2, 3 and M₁ ? {0, 1, 2, 3, 4}. Each entry in the conditional distribution should be expressed as a function of the parameters e and/or f.

d. Suppose M₁ = 1 and M₂ = 3. What are the possible numbers of stars if we assume no prior constraint on the values of N?

e. What is the most likely number of stars, given these observations? Explain how to compute this, or, if it is not possible to compute, explain what additional information is needed and how it would affect the result.

Transcribed Image Text:

M, м, F2 F2 F1 F1 M2 (м, M2 м, M1 F2 F1 (iї) (iї) (i)