In many applications, discrete-time random signals arise through periodic sampling of continuous-time random signals. We are concerned in this problem with a derivation of the sampling theorem for random signals. Consider a continuous-time, stationary, random process defined by the random variables {x_α(t)}, where t is a continuous variable. The auto correlation function is defined as

 and the power density spectrum is

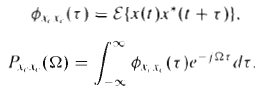
A discrete-time random process obtained by periodic sampling is defined by the set of random variables {x[n]}, where x[n] = x_α(nT) and T is the sampling period.

(a) What is he relationship between Ф_xx [n] and Ф_{xc xc} (τ)?

(b) Express the power density spectrum of the discrete-time process in terms of the power density spectrum of the continuous-time process.

(c) Under what condition is the discrete-time power density spectrum a faithful representation of the continuous-time power density spectrum?

Transcribed Image Text:

+ t)}. $u, v, ( 7 ) = E{x(1)x*(t P, (2) = Ps, x, ( 7 )e¯12rdt *dt.