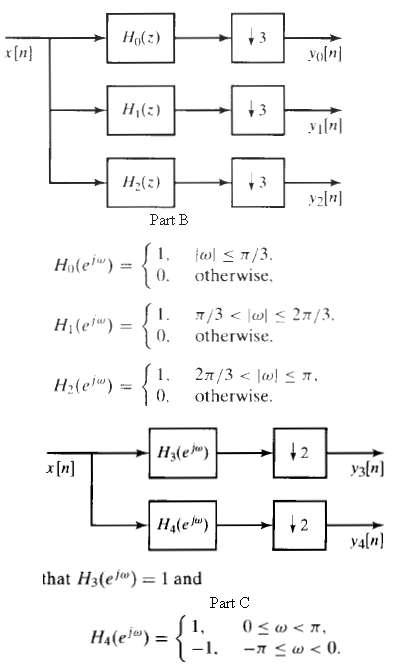
Consider the system in Figure with H₀(z), H₁(z), and H₂(z) as the system functions of LTI systems. Assume that x[n] is an arbitrary stable complex signal without any symmetry properties.

(a) Let H₀(z) = 1, H_1?(z) = z^?1, and H₂(z) = z^?2, Can you reconstruct x[n] from y₀[n], y₁[n], and y₂[n]? If so, how? If not, justify your answer.?

(b) Assume that H_0?(e^j?), H₁ (e^j?), and H_2?(e^j?) are as follows:?

Can you reconstruct x[n] from y₀[n], y₁[n], and y₂[n]? If so, how? If nor, justify your answer. Now consider the system in Figure. Let H₃(e^j?) and H₄(e^j?) be the frequency responses of the LTI systems in this figure. Again, assume that x[n] is an arbitrary stable complex signal with no symmetry properties.

(c) Suppose that H₃(e ^j?) = 1 and,?

can you reconstruct x[n] from y₃[n] and y₄[n]? If so, how? If not, justify your answer.

(el") = { 1. 27/3

Transcribed Image Text:

Ho(2) +3 x{n} voln) H(:) +3 H(2) 13 yaln] Part B 1, Hole") = { twl s7/3. otherwise, 0. { 1. 7/3 < |w) < 27/3. H(e") = 0. otherwise. H>(el") = { 1. 27/3 < lwl Sn. 0. otherwise. H3(e) x[n] y3{n] H,(e) 12 va[n) that H3(el") = 1 and Part C HA(el) = -1. 0