For zero mean, jointly Gaussian random variables, X₁, X₂, X₃, X₄, it is well known that

E(X₁X₂X₃X₄) = E(X₁X₂)E(X₃X₄) + E(X₁X₃)E(X₂X₄) + E(X₁X₄)E(X₂X₃)

Use this result to derive the mean-square value of r?_xx(m), given by (12.1.27) and the variance, which is?

var[r?_xx(m)] = E[|r?_xx(m)|²] - |E[r?_xx(m)]|²

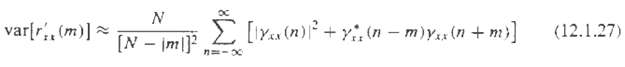
Transcribed Image Text:

var[r, (m)] E [IYa (n)+y, (n - m)y (n + m)] (12.1.27) [N - im|]?