Question: Freezing of a spherical drop (Figure 11B.10) to evaluate the performance of an atomizing nozzle, it is proposed to atomize a nonvolatile liquid wax into
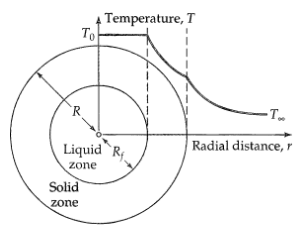
Freezing of a spherical drop (Figure 11B.10) to evaluate the performance of an atomizing nozzle, it is proposed to atomize a nonvolatile liquid wax into a stream of cool air. The atomized wax particles are expected to solidify in the air, from which they may later be collected and examined. The wax droplets leave the atomizer only slightly above their melting point. Estimate the time tf required for a drop of radius R to freeze completely, if the drop is initially at its melting point T0 and the surrounding air is at T∞. Heat is lost from the drop to the surrounding air according to Newton's law of cooling, with a constant heat-transfer coefficient h. Assume that there is no volume change in the solidification process. Solve the problem by using a quasi-steady-state method.
(a) First solve the steady-state heat conduction problem in the solid phase in the region between r = Rf (the liquid-solid interface) and r = R (the solid-air interface). Let k be the thermal conductivity of the solid phase. Then find the radial heat flow Q across the spherical surface at r = R.
(b) Then write an unsteady-state energy balance, by equating the heat liberation at r = Rt(t) resulting from the freezing of the solid to the heat flow Q across the spherical surface at r = R. Integrate the resulting separable, first-order differential equate, on between the limits 0 and R, to obtain the time that it takes for the drop to solidify. Let ∆Hf be the latent heat of freezing (per unit mass).
4 Temperature, T To -. Radial distance, r Liquid zone Solid zone
Step by Step Solution
3.52 Rating (182 Votes )
There are 3 Steps involved in it
Freezing of a spherical drop a The heat conduction equation for the solid phase i... View full answer
Get step-by-step solutions from verified subject matter experts
100% Satisfaction Guaranteed-or Get a Refund!
Document Format (1 attachment)
6-E-C-E-T-P (200).docx
120 KBs Word File
-
Access 30 Million+ textbook solutions.
-
Ask unlimited questions from AI Tutors.
-
Order free textbooks.
-
100% Satisfaction Guaranteed-or Get a Refund!
Study Help