Heat capacity from internal degrees of freedom

(a) Consider a two-level system with an energy splitting kB? between upper and lower states; the splitting may arise from a magnetic field or in other ways. Show that the heat capacity per system is the function is plotted in Fig. 11. Peaks of this type in the heat capacity are often known as Schottky anomalies. The maximum heat capacity is quite high, but for T > ? the heat capacity is low.?

(b) Show that for T >> ? we have C ? k_B?(?/2T)² + . . . . The hyperfine interaction between nuclear and electronic magnetic moments in paramagnetic salts (and in systems hating electron spin order) causes splittings with ? = 1 to 100mK. These splittings are often detected experimentally by the presence of a ten11 in 1/P in the heat capacity in the region T >> ?. Nuclear electric quadrupole interactions wit11 crystal fields also cause splittings, as in Fig. 12.

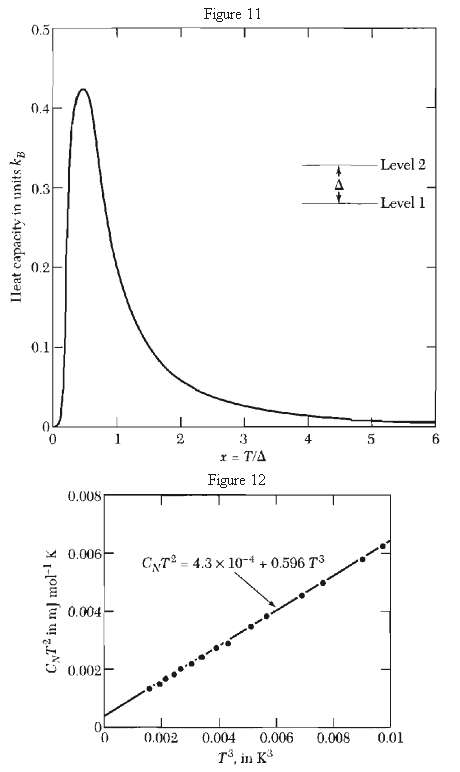
Ileat capacity in units k 0.5 0.4 0.3 0.2 0.1 CyT in m] mol- K 0.008 0.006 0.004 0.002 0 1 2 Figure 11 0.002 3 = T/A Figure 12 x = 4 CNT 4.3 10 +0.596 7 +A+ 0.004 0.006 0.008 T, in K -Level 2 10 5 -Level 1 0.01 6