I showed that at most one point on the particle trajectory communicates with r at any given time. In some cases there may be no such point (an observer at r would not see the particle--in the colorful language of General Relativity it is "beyond the horizon"). As an example, consider a particle in hyperbolic motion along the x axis: (In Special Relativity this is the trajectory of a particle subject to a constant force F = mc2/b.)

Sketch the graph of w versus t. At fbur or five representative points on the curve, draw the trajectory of a light signal emitted by the particle at that point--both in the plus x direction and in the minus x direction. What region on your graph corresponds to points and times (x, t) from which the particle cannot be seen? At what time does someone at point x first see the particle? (Prior to this the potential at x is evidently zero.) Is it possible for a particle, once seen, to disappear from view?

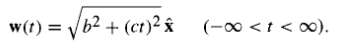
w(t) = b + (ct) * (-