In the absence of recurring fixed costs (such as those in exercise 12.4), the U-shaped cost curves we will often graph in upcoming chapters presume some particular features of the underlying production technology when we have more than 1 input.

A: Consider the following production technology, where output is on the vertical axis (that ranges from 0 to 100) and the inputs capital and labor are on the two horizontal axes. (The origin on the graph is the left-most corner).

(a) Suppose that output and input prices result in some optimal production plan A (that is not a corner solution). Describe in words what would be true at A relative to what we described as an isoprofit plane at the beginning of this chapter.

(b) Can you tell whether this production frontier has increasing, constant or decreasing returns to scale?

(c) Illustrate what the slice of this graphical profit maximization problem would look like if you held capital fixed at its optimal level k^A.

(d) How would the slice holding labor fixed at its optimal level ℓ^A differ?

(e) What two conditions that have to hold at the profit maximizing production plan emerge from these pictures?

(f) Do you think there is another production plan on this frontier at which these conditions hold?

(g) If output price falls, the profit maximizing production plan changes to once again meet the conditions you derived above. Might the price fall so far that no production plan satisfying these conditions is truly profit maximizing?

(h) Can you tell in which direction the optimal production plan changes as output price increases?

B: Suppose your production technology is characterized by the production function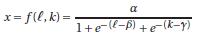

Where e is the base of the natural logarithm. Given what you might have learned in one of the end of-chapter exercises in Chapter 11 about the function x = f (ℓ) = α/(1+e^{−(ℓ−β)}), can you see how the shape in Graph 12.16 emerges from this extension of this function?

(a) Set up the profit maximization problem.

(b) Derive the first order conditions for this optimization problem.

(c) Substitute y = e^{−(ℓ−β)} and z = e^−(k−γ) into the first order conditions. Then, with the first order conditions written with w and r on the right hand sides, divide them by each other and derive from this an expression y(z,w,r) and the inverse expression z(y,w,r).

(d) Substitute y(z,w,r) into the first order condition that contains r. Then manipulate the resulting equation until you have it in the form az² +bz +c (where the terms a, b and c may be functions of w, r , α and p). (Hint: It is helpful to multiply both sides of the equation by r.) The quadratic formula then allows you to derive two “solutions” for z. Choose the one that uses the negative rather than the positive sign in the quadratic formula as your “true” solution z∗(α,p,w,r).

(e) Substitute z(y,w,r) into the first order condition that contains w and solve for y∗(α,p,w,r) in the same way you solved for z∗(α,p,w,r) in the previous part.

(f) Given the substitutions you did in part (c), you can now write e^{−(ℓ−β)} = y^∗(α,p,w,r) and e^−(k−γ) = z∗(α,p,w,r). Take natural logs of both sides to solve for labor demand ℓ(w,r,p) and capital demand k(w,r,p) (which will be functions of the parameters α, β and γ.)

(g) How much labor and capital will this firm demand if α = 100, β = γ = 5 = p, w = 20 = r? (It might be easiest to type the solutions you have derived into an Excel spreadsheet in which you can set the parameters of the problem.) How much output will the firm produce? How does your answer change if r falls to r = 10? How much profit does the firm make in the two cases.

(h) Suppose you had used the other “solutions” in parts (d) and (e) —the ones that emerge from using the quadratic formula in which the square root term is added rather than subtracted. How would your answers to (g) be different—and why did we choose to ignore this “solution”?

Transcribed Image Text:

a x= f(l, k) = 1+e-(l-p) +e(k-y)