Let us consider the use of the DFT (computed via the FFT algorithm) to compute the autocorrelation
Question:
Let us consider the use of the DFT (computed via the FFT algorithm) to compute the autocorrelation of the complex-valued sequence x(n), that is, Suppose the size M of the FFT is much smaller than that of the data length N. Specially, assume that N = KM.
(a) Determine the steps needed to section x(n) and compute rxx(m) for –(M/2) + 1 ≤ m ≤ (M/2) – 1, by using 4K M-point DFTs and one M-point IDFT
(b) Now consider the following three sequences x1(n), x2(n), and x3(n), each of duration M. Let the sequences x1(n) and x2(n) have arbitrary values in the range 0 ≤ n ≤ (M/2) – 1, but are zero for (M/2) ≤ n ≤ M – 1. The sequence x3(n) is defined as,
Determine a simple relationship among the M-point DFTs X1(k), X2(k), and X3(k).
(c) By using the result in part (b), show how the computation of the DFTs in part (a) can be reduce in number from 4K to 2K.
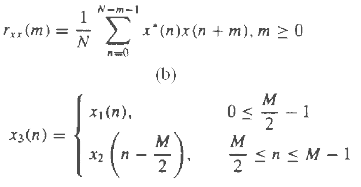
Step by Step Answer:

Digital Signal Processing
ISBN: ?978-0133737622
3rd Edition
Authors: Jonh G. Proakis, Dimitris G.Manolakis





