Let X 1 , X 2 , . . . , X n denote the outcomes of
Question:
Let X1, X2, . . . , Xn denote the outcomes of a series of n independent trials, where
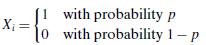
for i =1, 2, . . . , n. Let X = X1 + X2 +・ ・ ・+ Xn.
(a) Show that p̂1 = X1 and p̂2 = X/n are unbiased estimators for p.
(b) Intuitively, p̂2 is a better estimator than p̂1 because p̂1 fails to include any of the information about the parameter contained in trials 2 through n. Verify that speculation by comparing the variances of p̂1 and p̂2.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Mathematical Statistics And Its Applications
ISBN: 9780321693945
5th Edition
Authors: Richard J. Larsen, Morris L. Marx
Question Posted:





