Linear algebraic equations can arise in the solution of differential equations. For example, the following differential equation
Question:
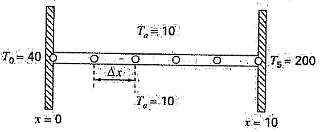
Linear algebraic equations can arise in the solution of differential equations. For example, the following differential equation derives from a heat balance for a long, thin rod (Figure):?
d2T/dx2 + h? (T? ? T) = 0
Where T = temperature (oC), x = distance along the rod (m), h? = a heat transfer coefficient between the rod and the ambient air (m ?2), and T? = the temperature of the surrounding air (oC). This equation can be transformed into a set of linear algebraic equations by using a finite divided difference approximation for the second derivative (recall Section 4.1.3),
d2T/dx2 = Ti+1 ? 2Ti + Ti-1/?x2
where Ti designates the temperature at node i. This approximation can be substituted into Eq. (P12.38) to give
-Ti-1 + (2 + h? ?x2)Ti ? Ti+1 = h? ?x2 Tu
This equation can be written for each of the interior nodes of the rod resulting in a tridiagonal system of equations. The first and last nodes at the rods ends are fixed by boundary conditions.
(a) Develop an analytical solution for Eq. (P12.38) for a 10-m rod with Tu = 20, T(x = 0) = 40, T(x = 10) = 200 and h? = 0.02.
(b) Develop a numerical solution for the same parameter values employed in (a) using a finite-difference solution with four interior nodes as shown in Figure. (?x = 2 m).
Step by Step Answer:

Numerical Methods For Engineers
ISBN: 9780071244299
5th Edition
Authors: Steven C. Chapra, Raymond P. Canale





