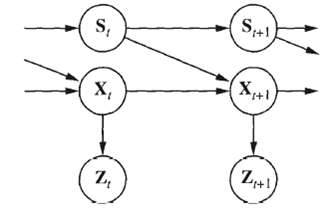
Often, we wish to monitor a Continuous-state system whose behavior switches unpredictably among a set of k distinct ?modes.? For example, an aircraft trying to evade a missile can execute a series of distinct maneuvers that the missile may attempt to track. A Bayesian network representation of such a switching Kalman filter model is shown in Figure.

a. Suppose that the discrete state S has k possible values and that the prior continuous state estimate P (X₀) is a multivariate Gaussian distribution. Show that the prediction P (X₁) is a mixture of Gaussians?that is. a weighted sum of Gaussians such that the weights sum to 1.

b. Show that if the current continuous state estimate P (X_t?e_{1: t}) is a mixture of in Gaussians, then in the general case the updated state estimate P (X_t+1?e_{1: t+1}) will be a mixture of km Gaussians.

c. what aspect of the temporal process do the weights in the Gaussian mixture represent? Together, the results in (a) and (b) show that the representation of the posterior grows without limit even for switching Kalman filters, which are the simplest hybrid dynamic models.

S41 S, X+1 , Z41)