A particle of mass m travels in a hyperbolic orbit past a mass M, whose position is
Question:
A particle of mass m travels in a hyperbolic orbit past a mass M, whose position is assumed to be fixed. The speed at infinity is v0, and the impact parameter is b (see Exercise 6).(a) Show that the angle through which the particle is deflected is(b) Let d? be the cross-sectional area (measured when the particle is initially at infinity) that gets deflected into a solid angle of size d? at angle ?.10 Show that This quantity is called the differential cross section. The term Rutherford scattering actually refers to the scattering of charged particles, but since the electrostatic and gravitational forces are both inverse-square laws, the scattering formulas look the same, except for a few constants.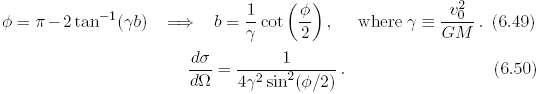
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





