Radial temperature gradients in an annular chemical reactor a catalytic reaction is being carried out at constant
Question:
Radial temperature gradients in an annular chemical reactor a catalytic reaction is being carried out at constant pressure in a packed bed between coaxial cylindrical walls with inner radius r0 and outer radius r1. Such a configuration occurs when temperatures are measured with a centered thermo well, and is in addition useful for controlling temperature gradients if a thin annulus is used. The entire inner wall is at uniform temperature T0, and it can be assumed that there is no heat transfer through this surface. The reaction releases heat at a uniform volumetric rate Sc throughout the reactor. The effective thermal conductivity of the reactor contents is to be treated as a constant throughout.
(a) By a shell energy balance, derive a second-order differential equation that describes the temperature profiles, assuming that the temperature gradients in the axial direction can be neglected. What boundary conditions must be used?
(b) Rewrite the differential equation and boundary conditions in terms of the dimensionless radial coordinate and dimensionless temperature defined as explain why these are logical choices.
(c) Integrate the dimensionless differential equation to get the radial temperature profile. To what viscous flow problem is this conduction problem analogous?
(d) Develop expressions for the temperature at the outer wall and for the volumetric average temperature of the catalyst bed.
(e) Calculate the outer wall temperature when r0 = 0.45 in., r1 = 0.50 in., keff = 0.3 Btu/hr ∙ ft ∙ F, T0 = 900°F, and Sc = 4800 cal/hr ∙ cm3.
(f) How would the results of part (e) be affected if the inner and outer radii were doubled?
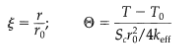
Step by Step Answer:






