Question: A random process X (t) is defined by X (t) = A cos (2? f c t), where A is a Gaussian-distributed random variable of

A random process X (t) is defined by X (t) = A cos (2? f c t), where A is a Gaussian-distributed random variable of zero means variance ?2A. This random process is applied to an ideal integrator, producing the output

(a) Determine the probability density function of the output Y (t) at a particular time tk.

(b) Determine whether or not Y (t) is stationary.

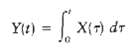
= X(-) dr Y(t)

Step by Step Solution

★★★★★

3.35 Rating (170 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The integrator output at time t is Yt XT dT 0 A cos2ft dr 0 Therefore A E Y t sin2 ft sin2nf t 2... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

19-E-T-E-C-S (3).docx

120 KBs Word File

Students Have Also Explored These Related Telecommunication Engineering Questions!

The joint probability density function of X and Y is given by f (x, y) = 6/7(x2 + xy/2) 0 Y}. (c) Find P{Y > 1/2|X

The joint probability density function of X and Y is given by f (x, y) = e(x+y) 0 x

A random process X (t) is said to be mean square continuous at some point in time t, if (a) Prove that X (t) is mean square continuous at time if its correlation function RX, X (t1, t2), is...

do the following,..... Write program that reads a person's first and last names, separated by a space. Then the program outputs last name, comma, first name. Create program that takes in user input...

In this computer experiment we study the statistical characteristics of a random process X (t) defined by X (t) = A cos (2?? c t + ?) + W (t). Where the phase ? of the sinusoidal component is a...

I just want to check my answer before I submitted it. The random process X (0:33" is a family of exponentials dependending on the random variable a. (a) Draw three sample functions of this random...

Help me obtain solutions Suppose that the random variable X follows an exponential distribution with probability density function f(x=20-", ocx 0). Define a new random variable V = X 3 (i) (a) Show...

A random process An experiment has been conducted for four treatments with eight blocks. Complete the following analysis of variance table (to 2 decimals but p-value to 4 decimals, if necessary). If...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

Business Research MethodologyQuestion Bank 1 1. When the marketing department of an organization attempts to determine the amount of time the managers in this department spend at their computers in...

In a manufacturing company, overhead allocations are made for three reasons: (1) to determine the full cost of a product; (2) to encourage efficient resource usage; and (3) to compare alternative...

Discuss the decision to use the atomic bomb on Hiroshima and Nagasaki.

Conv ert from logarithmic form to exponential form. a C lg 100000 5 lg 1 Ig 1000 =-3 e lgx = 1.7 b lg 10 1 d lgx=7.5 f lgx=-0.8

Ann and Bob form Robin Corporation. Ann transfers property worth $420,000 (basis of $150,000) for 70 shares in Robin Corporation. Bob receives 30 shares for property worth $165,000 (basis of $30,000)...

Which of these sets spans R3? That is, which of these sets has the property that any three-tall vector can be expressed as a suitable linear combination of the set's elements? (a) (b) (c) (d) (e) 001...

Auditors make materiality judgments during the planning phase of the audit in order to be sure they ultimately gather sufficient evidence during the audit to provide reasonable assurance that the...

John organized Toucan Corporation 10 years ago. He contributed property worth $1 million (basis of $200,000) for 2,000 shares of stock in Toucan (representing 100% ownership). John later gave each of...

Some audit firms develop very specific guidelines, either through quantitative guidelines or in tables, relating planning materiality to the size of sales or assets for a client. Other audit firms...

Probability that you roll a 3 or a 5. If you roll a die, the probability of each of the six possible outcomes (1, 2, 3, 4, 5, 6) is 1/6. What is the probability that you roll a 3 or a 5?

Contrast the function of application software with that of interconnection software.

What are the differences between digital and analog communication systems?

Contrast PDF and Postscript document formats.

Contrast CRT and LCD display monitors.

What is digital video?

If the spot rate for Canadian dollars is 1.25 dollars equals 1 US $, and the annual interest rate on fixed rate one-year deposits of Canadian dollars is 2.5% and for US$ is 1.5%, what is the...