Recall that the Fourier transform of x(t) = e j0 is X(j) = 2( 0

Recall that the Fourier transform of x(t) = e^jΩ0 is X(jΩ) = 2πδ(Ω – Ω₀) and the Fourier transform of:

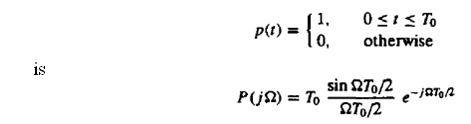
(a) Determine the Fourier transform Y(jΩ) of 

Y(t) = p(t)e^jΩ0t

And roughly sketch |Y(jΩ)| versus Ω.

(b) Now consider the exponential sequence 

x(n) = e^jω0n

where ω₀ is some arbitrary frequency in the range 0 < ω₀ < π radians. Give the most general condition that ω₀ must satisfy in order for x(n) to be periodic with period P (P is a positive integer).

(c) Let y(n) be the finite-duration sequence

y(n) = x(n)ω_N(n) = e^jω0nω_N(n)

Where ω_N(n) is a finite-duration rectangular sequence of length N and where x(n) is not necessarily periodic. Determine Y(ω) and roughly sketch |Y(ω)| and roughly sketch |Y(ω)| 0 ≤ ω ≤ 2π. What effect does N have in |Y(ω)|? Briefly comment on the similarities and differences between |Y(ω)| and |jΩ)|.

(d) Suppose that 

x(n) = e^j(2π/P)n               P a positive integer

and 

y(n) = ω_N(n)x(n)

where N = l P, l a positive integer. Determine and sketch the N-point DFT of y(n). Related your answer to the characteristics of |Y(ω)|.

(e) Is the frequency sampling for the DFT in part (d) adequate for obtaining a rough approximation of |Y(ω)|directly from the magnitude of the DFT sequence |Y(k)|? If not, explain briefly how the sampling can be increased so that it will be possible to obtain a rough sketch of |Y(ω)| from an appropriate sequence |Y(k)|.

Transcribed Image Text:

0sIs To 1, p(t) = otherwise is sin 2To/2 ΩΤΤ P(jN) = To -/QTO2